ICSE Set Set1 Year Icse Maths98 Set1.php Mathematics Exam Paper for students online
| Answers of this paper >> |
Mathematics
- 1998 ( I.C.S.E)
You are on Questions
Maximum Time : Two and Half Hours
General Instructions :
-Answer to this paper must be
written on the paper provided separately.
-You will NOT be allowed to write during the first fifteen minutes.
-This time is to be spent in reading the question papers.
-The time given at the head of this paper is the time allowed for writing the
answers .
-This Question Paper is divided into two sections.
-Attempt all questions from Section - A and any 4 questions from Section - B.
-The intended marks for questions or for any parts of questions are given in
brackets [ ].
-All working, including rough work should be done on the same sheet as the rest
of the answer.
-Ommission of essential working will result in loss of marks.
-Mathematical papers are provided.
Section - A
Q1. A man invests Rs. 46,875 at 4% Per annum compound interest for 3 years. Calculate :
(i) The interest for the 1st year
(ii) The amount standing to his credit at the end of the 2nd year.
(iii) The interest for the 3rd year.
Q2. A shopkeeper allowed a discount of 20% on the
marked price of an article, and sold it for Rs. 896. Calculate:
(i) His marked price ;
(ii)By selling the article at the discounted price, if he still gains 12% on his
cost price, what was the cost price ?
(iii) What would have been his profit %, if he had sold the article at the
marked price ?
Q3. On a map drawn to a scale of 1 : 25000, a
rectangular plot of land, ABCD, has the following measurements, AB = 12cm &
BC= 16cm . Angles A,B,C & D are all 90o each. Calculate:
(i) The diagonal distance of the plot in km.
(ii) The area of the plot in sq. km .
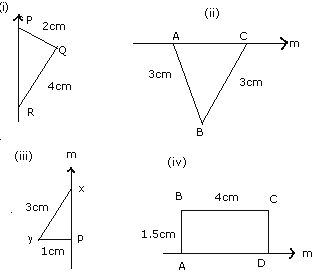
Q4. Part of a Geometrical figure is given in each of the diagrams below.
Complete the figures so that the line 'm' , in each case , is the line of
symmetry of the completed figure. Recognizable free hand sketches would be
awarded full marks.
Q5. The wheel of a cart is making 5 revolutions
per second. If the diameter of the wheel is 84 cm, Find its speed in km/hr. Give
your answer correct to the nearest km.
Q6. Ruler and compasses only may be used in this question. All construction lines and arcs must be clearly shown, and be of sufficient length and clarity to permit assessment.
(i) Construct a triangle ABC, in Which BC= 6cm,
AB= 9cm and angle ABC = 60o ;
(ii) Construct the locus of all points inside triangle ABC, which are
equidistant from B and C.
(iii) Construct the locus of the vertices of the triangles with BC as base,
Which are equal in area to triangle ABC.
(iv) Mark the point Q, in your construction, which would make QBC equal in
area to ABC, and isosceles.
(v) Measure and record the length of CQ.
Q7. A point P (a,b) is reflected in the X-axis to
p' (2,-3). Write down the values of a and b. P" is the image of P, when
reflected in the Y-axis. Write down the coordinates of P". Find the
coordinates of P'", when P is reflected in the line , parallel to the
Y-axis, such that x= 4.
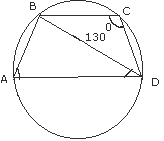
Q8 (a). In the figure given above, AD is the diameter of the circle . If BCD = 130O calculate:
(i)đ DAB (ii)đ ADB.
(b) State the locus of a point in a rhombus ABCD, which is equidistant
(i) From AB and AD ;
(ii) From the vertices A and C.
Q9. (a) Evaluate the following using tables:
[0.284 x Í
(136.78)] / (4.2)2
(b) Find the value of x and y, if
| [ | 1 | 2 | ] |
[ |
x | 0 | ] | ] |
[ |
x | 0 | ] |
| 3 | 3 | 0 | y | 9 | 0 |
(c) Solve the following in equation and graph the solution set, on the number line :
2x
- 3 < x + 2 <
3x + 5, x ╬
R
Q
10. (a) If a function in x is defined by f(x)
= x /( x2+1)
and x ╬
R, find :
(i)
f (1 /x), x ╣
0
(ii) f (x-1).
(b) The center O, of a circle has the coordinates (4, 5) and one point on the circumference is (8, 10). Find the coordinates of the other end of the diameter of the circle through this point.
(c)
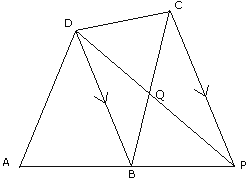
In
the figure given above, ABP is a straight line. BD is parallel to PC. Prove that
the quadrilateral ABCD is equal in area to triangle APD.
Q 11 (a) Use a graph paper for the question. Draw this graph of 2x - y - 1 = 0, and 2x + y = 9, on the same axes. Use 2 cm = 1 unit on both axes and plot only 3 point per line.
Write down the coordinates of the point of intersection of the two lines.
(b)
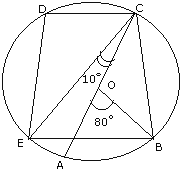
In the diagram given above, AC is the diameter of the circle, with centre O. CD and BE are parallel. Angle AOB = 80o and angle ACE = 10o
calculate :
(i) Angle
BEC,
(ii) Angle BCD,
(iii) Angle CED
Q
12. (a) A company with 10,000 shares of Rs. 100/- each declares an annual
dividend of 5 %.
(i) What is
the total amount of dividend paid by the company ?
(ii) What would be the annual income of a man, who has 72 shares, in the company
?
(iii) If he received only 4 % on his investment, find the price he paid for each
share.
(b) Find
the equation of a line, which has the y intercept 4, and is parallel to the line
2x - 3y = 7. Find the coordinates of the point. where it cuts the x - axis.
(c) Given below are the weekly wages of 200 workers in a small factory :
Calculate the mean weekly wages of the workers.
| Weekly wages in Rs. | No. of workers |
| 80 - 100 | 20s |
| 100 - 120 | 30 |
| 120 - 140 | 20 |
| 140 - 160 | 40 |
| 160 - 180 | 90 |
Q 13 (a)
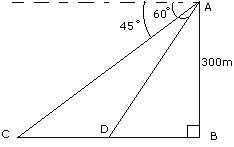
The
figure drawn above is not to the scale. AB is a tower, and two objects C & D
are located on the ground, on the same side of AB. when observed from the
top A of the tower, there angle of depression are 450 and 600.
Find the distance of the two objects. if the height of the tower is 300 mtr.
Give your answer to the nearest meter.
(b) The daily profits in rupees of 100 shop in a department store are distributed as follows :
| Profit per shop (Rs.) | No. of shops |
| 0 - 100 | 12 |
| 100 - 200 | 18 |
| 200 - 300 | 27 |
| 300 - 400 | 20 |
| 400 - 500 | 17 |
| 500 - 600 | 6 |
Draw
a histogram of the data given above, on graph paper & estimate the mode.
Q
14(a) Only and ruler and compasses may be used in this question. All
construction lines and arcs must be clearly shown and be of sufficient length
& clarity to permit assessment.
(I) Construct
a DABC,
such that AB = AC = 7 cm.
(II) Construct AD, the perpendicular bisector of BC.
(III) Draw a circle with centre A and radius 3 cm. Let this circle cut AD at P.
(IV) Construct another circle to touch
the circle with centre A, externally at P, and pass through B and C.
(b) The distance by road between two towns, A and B, is 216 km, and by rail it is 208 km. A car travels at a speed of x km/hr, and the train travels at a speed which is 16 km/hr faster than the car. Calculate :
(i)
The time taken by the car to reach town B from A, in terms of x;
(ii)
The time taken by the train to reach town B from A, in terms of x;
(iii) If the train takes 2 hours less than the car to reach town B, obtain an
equation in x, and solve it.
(iv) Hence find the speed of the train.
Q 15. (a) A solid consisting of a right circular
cone, standing on a hemisphere. is placed upright, in a right circular cylinder,
full of water, and touches the bottom. Find the volume of water left in the
cylinder, having given that the radius of the cylinder is 3 cm. and its height
is 6 cm ; the radius of the hemisphere is 2 cm. and the height of the cone is 4
cm. Give your answer to the nearest cubic centimeter. [Take
p = 22/7]
(b) Attempt this question on a graph paper. The
table shows the distribution of the daily wages, earned by 160 workers in a
building site.
| Wages in Rs. per day | No. of workers |
| 0 - 10 | 12 |
| 10 - 20 | 20 |
| 20 - 30 | 30 |
| 30 - 40 | 38 |
| 40 - 50 | 24 |
| 50 - 60 | 16 |
| 60 - 70 | 12 |
| 70 - 80 | 8 |
Using a scale of 2 cm. to represent 10 Rs., and 2 cm. to represent 20 workers, plot these values, and draw a smooth ogive, through the points. Estimate from the graph -
(i) The Median wage ;
(ii) The upper and lower quartile wage earned by the workers.
| Answers of this paper |

