ICSE Set Qa1 Year Icse Maths98 Qa1.php Mathematics Exam Paper for students online

Share On : Facebook Google+ LinkedIn Twitter

Latest for students online. All these are just samples for prepration for exams only. These are not actual papers.

Mathematics - 1998 ( I.C.S.E)
You are on Answers 1 to 5

Q1. A man invests Rs. 46,875 at 4% Per annum compound interest for 3 years. Calculate :
(i) The interest for the 1st year
(ii) The amount standing to his credit at the end of the 2nd years.
(iii) The interest for the 3rd year.

Ans . (i) P= Rs. 46,875
R=4% per annum
T= 1 year

A= 46,875 [ 1+ 4/100 ]¹
=46875 ( 104/100 )¹

= Rs 48,750

C.I =48,750-46,875

=Rs. 1,875

(ii)

A=P [ 1+R/100 ]^N
= 46,875[ 1+4/100]²
= 46,875 x ( 104/100) x ( 104/100 )
=Rs. 50,700
C. I. = 50700 - 46875
= 3825

(iii)

A=P[ 1+ R/100]^N
= 46,875 [ 1+ 4/100 ]³
=46,875( 104/100 )³
= 46,875 x 1.12 = Rs 52500 Interest for third yr. means

C.I = 52,500- 46,875 = 5625 = Interest till third yr- Interest till IInd year
= 5625-3825
=1800

Q2. A shopkeeper allowed a discount of 20% on the marked price of an article, and sold it for Rs. 896. Calculate:

(i) His marked price ;

(ii)By selling the article at the discounted price, if he still gains 12% on his cost price, what was the cost price ?

(iii) What would have been his profit %, if he had sold the article at the marked price ?

Ans . Discount = 20%
Let M.P. = x
S.P.= Rs. 896
Discount = 20% of x

(i) M.P. = S.P.+ Discount
or
x = 896 + 20/100 x
= Rs. 1120

(ii) Gain = 12%
C.P. = (S.P.x 100) / (100 + gain%)
= (896 x100) / (100 + 12) =Rs. 800

(iii) When S.P.= M.P.
= 1120
= ( 1120-800/800)¹⁰⁰ = 320/8
=40%

& C.P.=Rs. 800

Gain % = [(S.P. x 100)/C.P.] - 100
= [(1075.2 x 100)/800] - 100 =34.4 %

Q3. On a map drawn to a scale of 1 : 25000, a rectangular plot of land, ABCD, has the following measurements, AB = 12cm & BC= 16cm . Angles A,B,C & D are all 90^o each. Calculate:
(i) The diagonal distance of the plot in km.
(ii) The area of the plot in sq. km .

Ans. Scale 1: 25000

AB= 12cm, BC= 16cm

After conversion

AB= 3km , BC= 4km

AC= � (AB² + BC²)

= � (3²+4²)=5 km

Area= 3 x 4= 12 km²

Q4. Part of a Geometrical figure is given in each of the diagrams below. Complete the figures so that the line 'm' , in each case , is the line of symmetry of the completed figure. Recognizable free hand sketches would be awarded full marks.

Ans. Complete symmetrical figure about line m are.

Q5. The wheel of a cart is making 5 revolutions per second. If the diameter of the wheel is 84 cm, Find its speed in km/hr. Give your answer correct to the nearest km.

Ans.Diameter of the wheel=84cm

It's radius r = 84
.....................2

= 42cm = 0.00042 km

No. of revolutions made per second = 5, no. of rev/hr= 5x60x60 = 18,000/hr

No. of revolutions made per hour = 5/ (60 x 60) = .00138 per hour.
speed = ( Distance / time)
Distance = (2 x 22 x 0.0264) / 7 km speed = no. of rev/hr x distance in km
speed = 0.0264 / 0.00138 = 19.13 km/hr. = 18,000 x 22/7 x 2 x 0 .00042
................................................................. = 18 x 22 x 2 x 6/100
.................................................................speed = 47.52 km/hr

Q6. Ruler and compasses only may be used in this question. All construction lines and arcs must be clearly shown, and be of sufficient length and clarity to permit assessment.

(i) Construct a triangle ABC, in Which BC= 6cm, AB= 9cm and angle ABC = 60^o ;

(ii) Construct the locus of all points inside triangle ABC, which are equidistant from B and C.

(iii) Construct the locus of the vertices of the triangles with BC as bsase, Which are equal in area to triangle ABC.

(iv) Mark the point Q, in your construction, which would make QBC equal in area to ABC, and isosceles.

(v) Measure and record the length of CQ.

Ans. (i) Steps of construction

(a) Draw a line BC = 6cm
(b) Draw �CBA = 60^o(c) With center B & radius 9cm mark an arc cutting � CBX at A.
(d) join AC

Hints are given.Now draw the required triangle ABC.

(ii) Draw the perpendicular bisector of BC, AC, & AB intersecting at a point O.
Point 'O' is the required locus of all points inside triangle ABC.

(iii) Draw a circle in which AB is the diameter & O is the mid point of AB
With center A make an angle equal to angle ABC intersecting circle at point Q.

Point Q is the locus of the vertices of the triangle.

(iv) Draw a circle in which AB is the diameter and O is the mid point of AB.
With center A make an angle equal to angle ABC intersecting circle at point Q.
Area of triangle QBC = Area of triangle ABC & Isosceles.

(v) Measure the length of CQ from the figure.

Q7. A point P (a,b) is reflected in the X-axis to p' (2,-3). Write down the values of a and b. P" is the image of P, when reflected in the Y-axis. Write down the coordinates of P". Find the coordinates of P'", when P is reflected in the line , parallel to the Y-axis, such that x= 4.

Ans. The values of a = 2 & b=3
The coordinates of P" = (-2,-3)
When P is reflected in the line parallel to the Y-axis i.e. Y= 0
Then the coordinates of P"' = ( 2, 3)

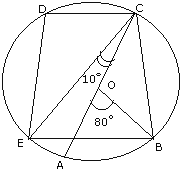
Q8 (a). In the figure given above, AD is the diameter of the circle . If BCD = 130^O calculate:

(i)� DAB (ii)� ADB.

(b) State the locus of a point in a rhombus ABCD, which is equidistant

(i) From AB and AD ;

(ii) From the vertices A and C. Ans. (a)

(i)� DAB = 180^o -130^o

=50^o

(ii)� ADB= 180^o-� DAB - �ABD^{(angle in a semicircle is a right angle)}

=40^o

=180^o - 50^o -90^o

(b) (i) Locus is point 0

(ii)Locus is point 0

SECTION-B

Q9. (a) Evaluate the following using tables:

[0.284 x � (136.78)] / (4.2)²

(b) Find the value of x and y, if


[	1	2	]	[	x	0	]	]	[	x	0	]
	3	3			0	y				9	0

(c) Solve the following in equation and graph the solution set, on the number line :

2x - 3 < x + 2 < 3x + 5,x � R

Ans (a). [0.284 x �(136.78)] / (4.2)²

=( 0.284 X 11.695 ) / 17.64 =0.188

(b)

[	1	2	]	[	x	0	]	=	[	x	0	]
	3	3			0	y				9	0

[	X	2Y	]	=	[	X	0	]
	3X	3Y				9	0

As the two matrixes are equal there elements must also be equal.

x = x , 2y = 0

3x = 9 , 3y = 0

from these we get x = 3 & y = 0

2x-3 <x+2 & x+2 � 3x+5

x 2x-3-2 & 3x+5 � x+2

x2x-5 & 2x � -3

52x-x &-3 � 2x

5x &-3/2 � x

5X & -1.5 � x

x= (-1,1,2,3,4)

Q 10. (a) If a function in x is defined by f(x) = x /( x²+1) and x � R, find :

(i) f (1 /x), x � 0
(ii) f (x-1).

(b) The center O, of a circle has the coordinates (4, 5) and one point on the circumference is (8, 10). Find the coordinates of the other end of the diameter of the circle through this point.

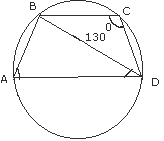
(c)

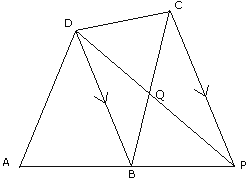
In the figure given above, ABP is a straight line. BD is parallel to PC. Prove that the quadrilateral ABCD is equal in area to triangle APD.

Ans.(a) f(x) = x /( x² + 1 )

(i) f ( 1/x ) = [( 1 /x)] / [(1/x)² + 1]
= (1/x) / [(1/x)² + 1] = x / (1 + x² )

(ii) f ( x - 1) = (x - 1) / [(x - 1)² + 1] = (x - 1) / (x² - 2x + 2)

(b) Let P(x,y) be the coordinates of the other end of the diameter .

According to section formula , the coordinates of P (x,y) are :-

(8+x) / 2 = 4

x= 8-8

(10+y)/2 = 5

10+y =10

y= 0

Hence the coordinates of the other end of the diameter are P(0,0).

To Prove :- Area of triangle APD = area of Quadrilateral ABCD

Proof :- Triangle BDC & triangle BDP are on the same base DB & between same parallels DB & CP

Therefore area of triangle BDC = area of triangle BDP -------(i)

Subtracting area of triangle DBQ from both sides of equation (i)

Area of triangle BDC - Area of triangle DBQ = area of triangle BDP - area of triangle DBQ

Area of triangle DQC = area of triangle BQP -----------(ii)

Adding area of quadrilateral DABQ on both sides of equation (ii) We get

area of triangle DQC + area of quadrilateral DABQ = area of triangle BQP + area of quadrilateral DABQ

area of quadrilateral ABCD = area of triangle APD.

Q 11 (a) Use a graph paper for the question. Draw this graph of 2x - y - 1 = 0, and 2x + y = 9, on the same axes. Use 2 cm = 1 unit on both axes and plot only 3 point per line.

Write down the coordinates of the point of intersection of the two lines.

(b)

In the diagram given above, AC is the diameter of the circle, with centre O. CD and BE are parallel. Angle AOB = 80^o and angle ACE = 10^o

calculate :
(i) Angle BEC,
(ii) Angle BCD,
(iii) Angle CED

Ans.(A) 2X-Y-1=0

2X+Y=9

(i) 2X-Y-1=0

2X-Y=1

^X	⁰	¹	²
^Y	^-1	¹	³

^{(ii)
2X+Y=9}

^Y=9-2X

^X	⁰	¹	^-1
^Y	⁹	⁷	¹¹

Now draw the graph using these two tables. pt. of intersection will be (2.5, 4)

(b)

(i)�BEC =50^o

(ii) �BCD =100^o

(iii) �CED = 30^o

Q 12. (a) A company with 10,000 shares of Rs. 100/- each declares an annual dividend of 5 %.

(i) What is the total amount of dividend paid by the company ?

(ii) What would be the annual income of a man, who has 72 shares, in the company ?

(iii) If he received only 4 % on his investment, find the price he paid for each share.

(b) Find the equation of a line, which has the y intercept 4, and is parallel to the line 2x - 3y = 7. Find the coordinates of the point. where it cuts the x - axis.

(c) Given below are the weekly wages of 200 workers in a small factory :

Calculate the mean weekly wages of the workers.

Weekly wages in Rs.	No. of workers
80 - 100	20s
100 - 120	30
120 - 140	20
140 - 160	40
160 - 180	90

Ans. (a) Total no. of shares of a company = 10, 000
Cost of one share = Rs. 100
Therefore total cost of 10,000 shares = 10,000 x 100
= 1,000,000
Dividend = 5%

(i) Total amount of dividend paid by the company = ( 1,000,000 x 5 ) / 100
= Rs. 50,000

(ii) Number of shares of a man in the company = 72
Cost of one share =Rs. 100
Therefore total amount invested by man =72 x 100
= Rs 7200
Annual income of man =( 7200 x 5 ) / 100
= Rs. 360

(iii) If dividend =4%
Annual income of man = Rs. ( 7200 x4 ) / 100
= Rs. 288
The price paid by man = Rs. ( 288 / 72)
= Rs. 4

(b) The given line is 2X-3Y =7
Its slope = 2/3
and y intercept = -7
Slope of a line Parallel to it = 2 /3
The equation of a line through (0,4) & parallel to the line is

y-4 = 2 (x-0)
..........3

3y-12= 2x

i.e 3y-2x-12 =0 it cuts the x-axis at (6,0)

(c)

Weekly Wages in Rs.	Mid of wages X	No. of workers W	X.W
80-100	90	20	1800
100-120	110	30	3300
120-140	130	20	2600
140-160	150	40	6000
160-180	170	90	15300
Total		200	29000

Mean weekly wage = XW/W

= 2900
....200

=Rs. 14.50

Q 13 (a)

The figure drawn above is not to the scale. AB is a tower, and two objects C & D are located on the ground, on the same side of AB. when observed from the top A of the tower, there angle of depression are 45⁰ and 60⁰. Find the distance of the two objects. if the height of the tower is 300 mtr. Give your answer to the nearest meter.

(b) The daily profits in rupees of 100 shop in a department store are distributed as follows :

Profit per shop (Rs.)	No. of shops
0 - 100	12
100 - 200	18
200 - 300	27
300 - 400	20
400 - 500	17
500 - 600	6

Draw a histogram of the data given above, on graph paper & estimate the mode.

Ans. (a)

Let the distance between two objects C&D is X

In D ADB

tan 60^o= AB / BD
1.732= 300 /BD
BD = 300 / 1.732
=173.20 m

In ABC

tan 45^o = AB / CB
1= 300 / (X + BD)
X+BD =300

X+ 173.20 =300

X= 300-173.20

=126.8m

Hence the distance between the objects C & D is 126.8ms

(b)

Profit per shop (in Rs.)

No. of shops

0-100

100-200

200-300

300-400

400-500

500-600

Now plot the graph between no. of shops and profit per shop on the graph paper and obtain the mode from the histogram.

Q 14(a) Only ruler and compasses may be used in this question. All construction lines and arcs must be clearly shown and be of sufficient length & clarity to permit assessment.
(I) Construct a DABC, such that AB = AC = 7 cm.
(II) Construct AD, the perpendicular bisector of BC.
(III) Draw a circle with centre A and radius 3 cm. Let this circle cut AD at P.
(IV) Construct another circle to touch the circle with centre A, externally at P, and pass through B and C.

(b) The distance by road between two towns, A and B, is 216 km, and by rail it is 208 km. A car travels at a speed of x km/hr, and the train travels at a speed which is 16 km/hr faster than the car. Calculate :

(i) The time taken by the car to reach town B from A, in terms of x;
(ii) The time taken by the train to reach town B from A, in terms of x;
(iii) If the train takes 2 hours less than the car to reach town B, obtain an equation in x, and solve it.
(iv) Hence find the speed of the train.

Ans.(a) (I) steps of construction

(i) Draw a line BC=5cm

(ii) With center B& radius 7cm draw an arc C

(iii) With center C & taking same radius cut the previous arc at point A

(iv) Join AB & AC

ABC is the required triangle. Hints are given to you . You draw the required construction.

(II) Steps of construction

(i) With centre B & taking radius greater than 1/2 BC mark an arc C intersecting on BC at point D

(ii) Join AD .It is the required perpendicular bisector of BC.

(III) (Ans.) Take point A as a centre and radius = 3cm. Draw a circle cutting AD at P.

(IV) (ans.) Take point D as a centre and radius = BD draw a circle passing through B & C and touching the circle with centre A, externally at P.

(b) Distance by road between towns A & B = 216 km

Distance by rail between towns A & B= 208 Km

speed of a car = x km/hr.

speed of train = (x+16) km/hr.

(i) Time taken by the car = 216 / x hr

(ii) Time taken by train = 208 / (x + 16) hr

(iii) ( 216/x) -(208 /x) = 2

[216(x+16) - 208x] / x (x + 16) = 2

216x +3456-208x = 2x(x+16)

8x+3456= 2x² + 32x

2x² + 32x-8x-3456=0

2x²+24x-3456 +0

x²+12x-1728=0

x²+48x-36x - 1728= 0

x(x+48)-36(x+48)= 0

(x+48) (x-36)= 0

x= -48 & x=36

Neglecting negative value

(iv)Speed of the train = (x+16) km/hr

=(36+16) km/hr

=52 km/hr

Q 15. (a) A solid consisting of a right circular cone, standing on a hemisphere. is placed upright, in a right circular cylinder, full of water, and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm. and its height is 6 cm ; the radius of the hemisphere is 2 cm. and the height of the cone is 4 cm. Give your answer to the nearest cubic centimeter. [Take p = 22/7]
(b) Attempt this question on a graph paper. The table shows the distribution of the daily wages, earned by 160 workers in a building site.

Wages in Rs. per day	No. of workers
0 - 10	12
10 - 20	20
20 - 30	30
30 - 40	38
40 - 50	24
50 - 60	16
60 - 70	12
70 - 80	8

Using a scale of 2 cm. to represent 10 Rs., and 2 cm. to represent 20 workers, plot these values, and draw a smooth ogive, through the points. Estimate from the graph -

(i) The Median wage ;

(ii) The upper and lower quartile wage earned by the workers.

Ans. (a)

Volume of a cone = 1/3 p r² h
volume of hemisphere = 2/3 p r³
Total volume = 1/3 pr² h + 2/3 pr³
= 1 /3 pr²(h+2r)
= (1/3) x (22/7) x 2 x 2 (4+2x2)
= (88 / 21) x (8)
=33.52 cm³

Volume of water left in the cylinder

=Volume of cylinder - (volume of cone + hemisphere)

=pr²h - 33.52

= (22 / 7 x 9 x 6) -33.52
=169.714 - 33.52

=136.19 cm³

(b) Scale for Rs. 1:5 & scale for workers 1 : 10

Plotting the points (10, 12), (20,32), (30,62), (40, 100), (50,124),(60,140), (70,152), (80,160) & join them by a free hand curve we get an ogive curve .

(i) The median wage= 34.73

(ii) Lower quartile wage= 22.66

Upper quartile wage =123.33

Wages in Rs per day	No. of workers	Upper limit	C.F.	Ordered Pairs
0-10	12	10	12	(10,12)
10-20	20	20	32	(20,32)
20-30	30	30	62	(30,62)
30-40	38	40	100	(40,100)
40-50	24	50	124	(50,124)
50-60	16	60	140	(60,140)
60-70	12	70	152	(70,152)
70-80	8	80	160	(80,160)