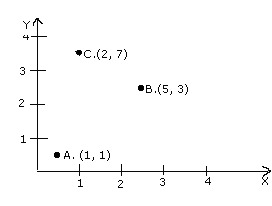ICSE Set Qa1 Year Icse Maths99 Qa1.php Mathematics Exam Paper for students online
| Q12.
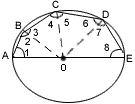
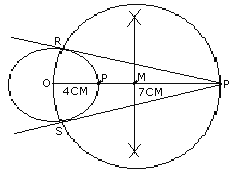
(a) In the figure given above ,AE is the
diameter of the circle .Write down the numerical value of angle ABC +
angle CDE. Ans. (a) ÐABC
= 90O (angle in a semi circle) therefore
Ð7+Ð8
= 90OÐ1=Ð2=Ð3=Ð4....=Ð8 (i) Draw a circle of radius = 4cm |
||||||||||||||||||||||||||||||||||||||||||||||||
| Q13.
(a) Given A ={a,b,c,d};B={1,2,3,4}, (i) From orderd pairs showing a 1 to 1 function from A to B; (ii)From ordered pairs showing a many to 1 function from A to B; (iii)Explain why it is not possible to construct ordered pairs which represent a many to 1 onto function from A to B. (b)With reference to the figure given alongside , a metal container in the form of a cylinder is surmounted by a hemisphere of the same radius .The internal height of the cylinder is 7 m and the internal radius is 3.5m Calculate : (i) the total area of the internal surface,excluding the base : (ii)the internal volume of the container in m3. 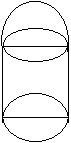
Ans. (a) A = {a, b, c,d}
B ={ 1, 2, 3, 4} (b) (i)Total internal surface area = 2prh
+3p
r2 |
||||||||||||||||||||||||||||||||||||||||||||||||
| Q14(a)
The center of a circle of radius 13 units is the point (3,6
).P(7,8)is a point inside the circle.APB is a chord of the
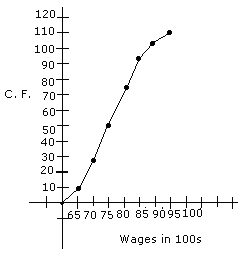
circle such that AP=PB .Calculate the length of AB. (b)Use the graph paper for this question.The table given below shows the monthly wages of some factory workers. (i)Using the table ,calculate the cumulative frequencies of workers. (ii)Draw the cumulative frequency curve .Use 2cm =Rs 500,Starting the origin at Rs. 6500 on x axis ,and 2cm =10 workers on the y-axis. (iii)Use your graph to write down the median wage in Rs.
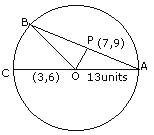 Solution to find :- OP2 = (7-3)2 + (9-6)2 Op2 = 16+9 OP2 = 25 OP = 5 Now in triangle OPA :- OA2 - OP2 = AP2 (13)2 -( 5)2 = AP2 169- 25 AP2 144 = AP2 AP = 12 Therefore PO = 12 AB = 12 + 12 = 24 units
|