ICSE Set Set1 Year Icse Maths97 Set1.php Mathematics Exam Paper for students online

Mathematics - 1997 ( I.C.S.E)
You are on Questions

General Instructions :
Time: Two & Half Hours

-Answer to this paper must be written on the paper provided separately.
-You will NOT be allowed to write during the first fifteen minutes.
-This time is to be spent in reading the question papers.
-The time given at the head of this paper is the time allowed for writing the answers .
-This Question Paper is divided into two sections.
-Attempt all questions from Section - A and any 4 questions from Section - B.
-The intended marks for questions or for any parts of questions are given in brackets [].
-All working, including rough work should be done on the same sheet as the rest of the answer.
-Ommission of essential working will result in loss of marks.
-Mathematical papers are provided.

Section - A

Q1. A person invests Rs. 5,600 at 14% p.a. compound  interest for 2 years.  Calculate :
(1)  The interest for the 1st year ;
(2) The amount at the end of the 1st year  
(3) The interest for 2nd year, correct to the nearest Rs.

Q2  Lessons on loss, profit and discount has been omitted from the syllabus w.e.f. year 2000

Q3. On a map drawn to a scale of 1:250000 a triangular plot of land has the following measurements:
AB = 3 cm,  BC = 4 cm,  Ð ABC = 90°. Calculate :
(1) the actual length of AB in km;
(2) the area of the plot in sq.km.
 

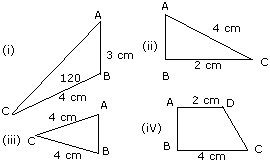
Q4. Part of a geometrical figure is given in each of the diagrams below.
Complete the figure so that the line AB in each case is a line of symmetry of the completed figure.
Give also the geometrical name for the completed figure.
Recognizable free hand sketches would be awarded full marks.

Q5. A Bucket is raised from a well by means of a rope which is wound round a wheel of diameter 77 cm. Given that the bucket ascends in 1 minute 28 seconds with a uniform speed of 1.1 m/s calculate the number of complete revolutions the wheel makes in raising the bucket .Take  p to be 22/7.

Q6.Ruler and compasses only may be used in this question. All construction lines and arcs must be clearly shown, and be of sufficient length  and clarity to permit assessment .
(i) Construct triangle ABC, in which BC = 8 cm, AB = 5 cm, angle ABC = 60^o ;
(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC ;
(iii) Construct the locus of point inside the triangle which are equidistant from B and C ;
(iV) Marks as P, the point which is equidistant from AB,BC and also equidistant from B and C ;
(V) Measure and record the length of PB.

Q7.(i) point P (a,b) is reflected in the x axis to P'(5,-2). Write down the value of a and b.
(ii)P'' is the image of P when reflected in the y axis. Write down the coordinates of P''.
(iii)Name a single transformation that maps P' to P''.

Q8.

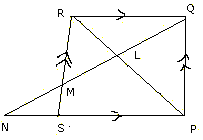
In the above figure, PQRS is a parallelogram ; PQ = 16 cm, QR = 10 cm. L is a point on PR such that RL : LP = 2:3. QL produced meets RS at M and PS produced meets at N.
(i) Prove that triangle RLQ is similar to triangle PLN. Hence find PN.
(ii) Name a triangle similar to triangle RLM. Evaluate RM as a fraction.

Q9.(a) State whether the following statements are TRUE or FALSE.
(i) If a b, then a-cb-c.
(ii) f a<b,then ac<bc.
(iii) If ab,then a/c b/c.
(iv) If a-c < b-d, then a+d < b+c.
where a,b,c,d are real number , c ¹ 0.
(b) Evaluate without using table :

Q10. (a)

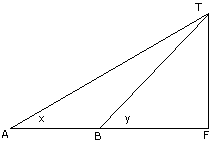
In the above figure, not  drawn to sale TF as a tower . The elevation of T from A is x , where tan x=2/5 and AF=200m. The elevation of T from B, where AB=80m, is y. Calculate :
(i) The height of a tower TF ;
(ii) The angle y,correct to the nearest degree.
(b.)  Ruler and compasses only may be used in this question.All construction lines and arcs must be clearly shown,and be of sufficient length and clarity to permit assessment.
(i) Construct triangle ABC, in which AB=9 cm, BC= 10 cm and angle ABC=45^o ;
(ii) Draw a circle, with centre A and radius 2.5 cm. Let it meet AB at D.
(iii) Construct a circle to touch the circle with centre A externally at D and also to touch the line BC.
(c) Calculate the distance between A(7,3) and B on the x-axis whose abscissa is 11.

Q11. (A.)   

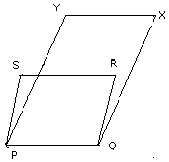
In the above figure ,PQRS and PQXY are parallelograms.
(i) Prove that SX ans RY bisect each other;
(ii)If SX=RY, prove that angle RSY =90^o.
(B.) Car A travels x Km. for every litre of petrol used by car B travels (x+5) Km. for every litres of petrol.
(i) Write down the number of litres of petrol used by car A and car B in covering a distance of 400 Km.
(ii)  If car A uses 4 litres of a petrol more than car B in covering the 400 Km. write down an equation in x and solve it to determine the number of litres of petrol used by car B for the journey.

Q12. (A.) The contents of 100 match boxes were checked to determine the number of matches they contained.
No of matches :       35     36     37      38     39     40     41
No of boxes    :       6       10     18     25      21     12     8
(i) Calculate ,correct ot one decimal place, the number of matches per box ;
(ii) Determine how many extra matches would have to be added to the total contents of the 100 boxes to bring mean up to the exactly 39 matches.
(B.) Use a graph paper for this question.
Draw the graph of  x + y + 2 = 0 and  3x - 4y =15 on the same axes.  Use 2 cm = 1 unit in both cases only three points per line.
Write down the coordinates of the point of  intersection of lines.

Q 13.(a) Attempt this question on a graph paper.
The table below shows the distribution of marks gained by a group of 400 students in an examination :
marks less than   10   20   30    40     50    60    70    80    90   100
no. of students     5    10   30     60   105   180  270  355  390   400
Using a scale of 2 cm to represent 10 marks and 2 cm to represent 50 students, plot these values and draw a smooth curve through the points.
Estimate from the graph  :   (i) the median mark  (ii) the quartile marks.
Q14. (A.) A lady holds 1800 shares each of Rs. 100 of a company that pays 15% dividend annually. Calculate her annual dividend.
If she has bought these shares at 40 % premium what  % return does she get on her investment ? Give your answer to the nearest integer.
(B.) A cylindrical can whose base is horizontal  and of radius 3.5 cm contains sufficient water so that when a sphere is placed in the can the water just covers the sphere. Given that the sphere just fits into the can. Calculate
(i) the total surface area of the can in contact with water  when the sphere is in it.
(ii) the depth of water in the can before the sphere was put into the can. Take p to be 22/7 and give your answer as proper fraction.

Q 15. (a) (i) The line 4x - 3y + 12 = 0 meets the x - axis at A . Write the coordinates of A.
(ii)  Determine the equation of the line passing through A and perpendicular to  4x - 3y + 12 = 0
(b)

In the figure given above A,D, B, C are four points on the circumference of a circle with centre O . Arc AB = 2 (arc BC) and angle AOB = 108^o. Calculate in degrees :
(i) angle  ACB,
(ii) Angle CAB  
(iii) angle ADB.
justify your calculation.